

I compiled on a single table the values I found from various articles and reviews over the web. For VII, a vectorized kernel is now used instead of a scalar one, with FP64 performance increasing a bit on the Scientific test as a result (sans FFT). The values in this table (and those for fp64 and fp128) are generated by the MATLAB function float_params that I have made available on GitHub and at MathWorks File Exchange.Here is the GFLOPS comparative table of recent AMD Radeon and NVIDIA GeForce GPUs in FP32 (single precision floating point) and FP64 (double precision floating point). If subnormal numbers were supported in the same way as in IEEE arithmetic, xmins would be 9.18e-41. (*) Unlike the fp16 format, Intel’s bfloat16 does not support subnormal numbers. The next table shows the unit roundoff, smallest positive (subnormal) number xmins, smallest normalized positive number xmin, and largest finite number xmax for the three formats. The program I hope to use most is Rhino 3d (which doesn't even need a legit FP64 GPU), but if I want to use programs which take advantage of FP64 in the. After doing some research, it looks like AMD cards generally perform better with FP64 vs. Note, single precision refers to a 32-bit representation for floating point numbers (sometimes called FP32), while double precision refers to a 64-bit. The drawback of bfloat16 is its lesser precision: essentially 3 significant decimal digits versus 4 for fp16. This paper proposes a method for implementing dense matrix multiplication on FP64 (DGEMM) and FP32 (SGEMM) using Tensor Cores on NVIDIAs graphics. Earlier, I was looking at Nvidia cards, and the issue of FP32 vs. On the other hand, when we convert from fp32 to the much narrower fp16 format overflow and underflow can readily happen, necessitating the development of techniques for rescaling before conversion-see the recent EPrint Squeezing a Matrix Into Half Precision, with an Application to Solving Linear Systems by me and Sri Pranesh. This post briefly introduces the variety of precisions and Tensor Core capabilities that the NVIDIA Ampere GPU architecture offers for AI training.
Operations using FP64 or one of the 16-bit formats are not affected and continue to use those corresponding types. Consequently, converting from fp32 to bfloat16 is easy: the exponent is kept the same and the significand is rounded or truncated from 24 bits to 8 hence overflow and underflow are not possible in the conversion. The variable affects only the mode of FP32 operations. And it has the same exponent size as fp32.
#FP32 VS FP64 PLUS#
The IEEE FP32 single precision format has an 8-bit exponent plus a 23-but mantissa and it has a smaller range of 1e-38 to 3e 38. Formatīfloat16 has three fewer bits in the significand than fp16, but three more in the exponent. The IEEE FP64 format is not shown, but it has an 11-bit exponent plus a 52-bit mantissa and it has a range of 2.2e-308 to 1.8e 308. The allocation of bits to the exponent and significand for bfloat16, fp16, and fp32 is shown in this table, where the implicit leading bit of a normalized number is counted in the significand.
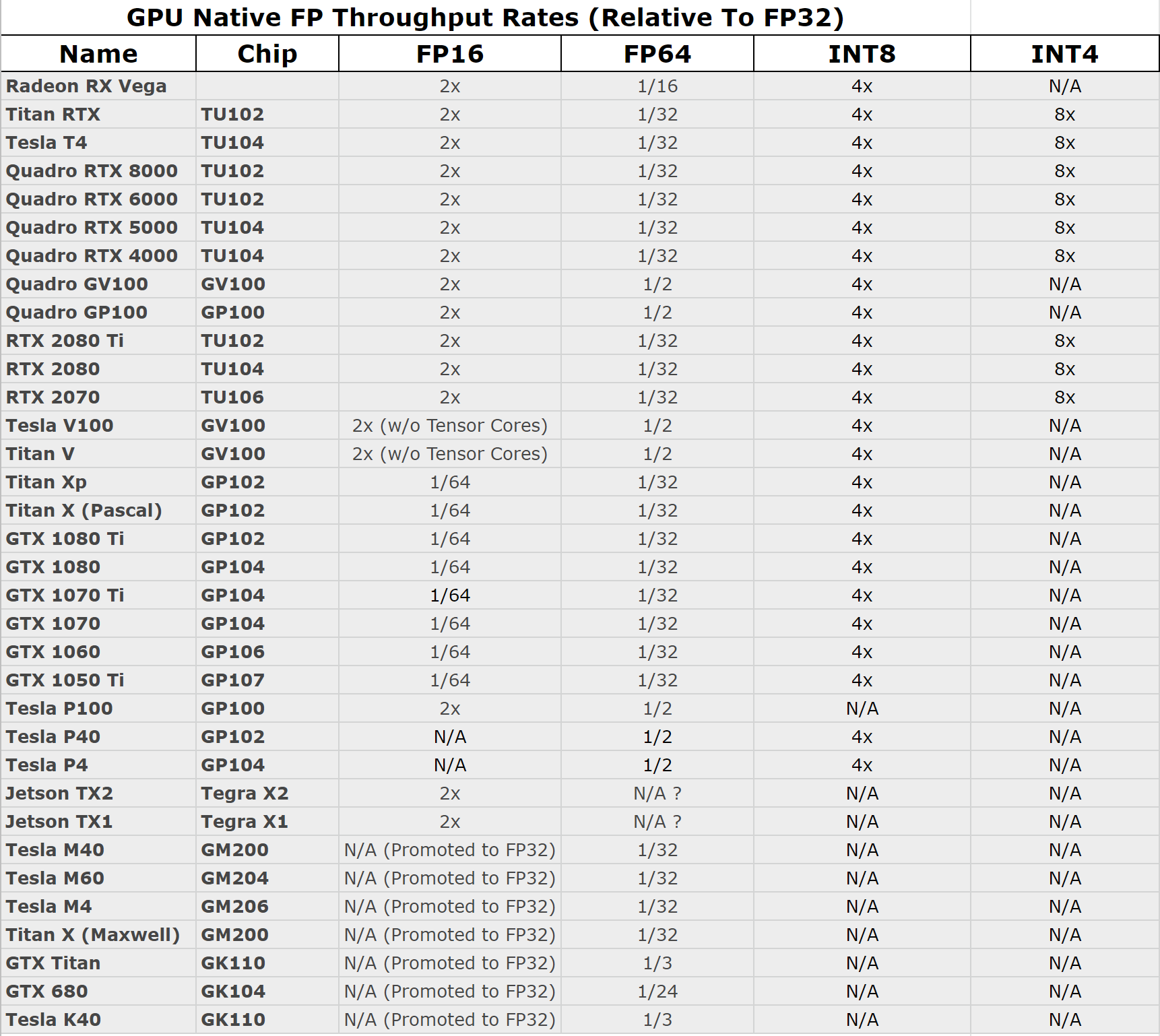
Intel, which plans to support bfloat16 in its forthcoming Nervana Neural Network Processor, has recently (November 2018) published a white paper that gives a precise definition of the format. The bfloat16 format is used by Google in its tensor processing units. Case in point is the matter of FP64 performance. This has led to the development of an alternative 16-bit format that trades precision for range. Recently,I want to summarize a list about core size and computation speed briefly.Such as the size and speed of these cores like FP32,INT32,INT16,INT8 and INT4.But I can’t find this type of information.When I searched, I always found the introduction about whole framework of gpu production, but little description in hardware details.If you know how can i find the information,please help me. Fp16 has the drawback for scientific computing of having a limited range, its largest positive number being.


 0 kommentar(er)
0 kommentar(er)
